강화학습을 이용한 주식투자란?

이전 장에서 현재까지의 강화학습은 주로 게임용 인공지능에 사용됐다고 했습니다. 그러나 강화학습이 적용될 수 있는 범위는 무궁무진합니다. 이번 장에서는 주식투자에 강화학습을 적용하는 방법을 알아보겠습니다.

직관적으로 강화학습 전략 알아보기

강화학습을 주식에 적용하는 방법을 어려운 수식이나 용어를 빼고 살펴봅시다. 강화학습으로 무작정 주식투자를 해보고 경험을 쌓아 잘한 경우에 긍정적으로 보상하고 잘못한 경우엔 부정적으로 보상함으로써 일일이 학습 데이터를 만드는 수고를 없애면서도 효과적으로 주식투자 머신러닝을 수행할 수 있는 전략을 알아봅니다.

강화학습을 이용한 주식투자 구조

주식투자도 어떠한 환경에서 매수(buy), 매도(sell), 관망(hold) 등을 판단하는 문제로서 강화학습을 적용할 수 있습니다. 주식투자에 강화학습을 적용했을 때 구성 요소는 다음과 같습니다.

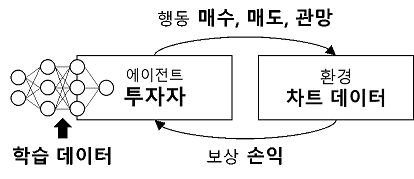
주식투자에서의 강화학습 개념도

주식투자 강화학습에서 에이전트는 행동을 수행하는 주체인 투자자 역할을 합니다. 행동은 매수, 매도, 관망 등이 있을 수 있습니다. 행동은 신경망으로 결정하고 신경망은 투자를 진행하면서 발생하는 보상과 학습 데이터로 학습합니다.

주식투자 강화학습에서의 환경은 다양하게 정할 수 있지만, 여기서는 한 종목의 차트 데이터를 환경으로 고려합니다. 에이전트가 수행하는 행동의 결과로 발생하는 수익 또는 손실을 보상으로 하여 신경망을 학습합니다.

차트 데이터 이해하기

차트 데이터는 어떠한 종목의 시가, 고가, 저가, 종가, 거래량 등 있는 그대로의 데이터입니다. 차트 데이터로 투자 손익을 계산합니다. 학습 데이터는 인공 신경망을 학습할 목적으로 가공한 데이터입니다. 차트 데이터와 학습 데이터에 대해서는 4.3절에서 상세히 다룹니다.

어떠한 차트 데이터상에서 투자자는 일명 묻지마 투자를 합니다. 마구잡이로 매수, 매도하는 것입니다. 그러면 일정 시간이 지났을 때 이익이나 손해가 발생하게 됩니다. 그 결과가 이익이면 보상, 손해면 처벌을 내림으로써 이전에 행했던 행동들을 학습 데이터와 보상으로 학습합니다. 시행착오를 반복하면서 에이전트의 인공 신경망은 점점 똑똑해지고 수익을 내는 방향으로 행동을 결정하게 됩니다.

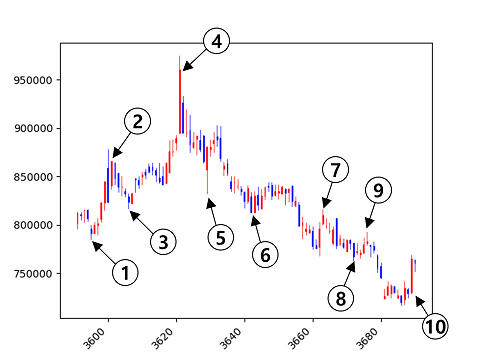
다음은 일봉 차트의 예입니다. 번호를 매긴 화살표가 가리키는 지점의 종가에서 어떤 투자 행동을 해야 할까요?

일봉 차트에서 투자 행동

직관적으로 1번에서는 매수, 2번에서는 매도, 3번에서 매수, 4번부터 9번까지는 매도 및 관망, 10번에서는 매수를 하면 괜찮은 수익을 낼 수 있을 것 같습니다.

차트 데이터를 바탕으로 강화학습을 하는 방식

이 차트에서 강화학습으로 무작정 투자 행동을 결정하고 어떤 식으로 학습할 수 있을지 살펴보겠습니다. 이 예제에서는 초기 자본으로 1,000만 원이 있고 거래에 대한 수수료와 세금은 고려하지 않고 1주씩만 매수하거나 매도한다고 제한합니다. 그리고 2%의 손익이 발생했을 때 보상을 줍니다. 다음 표는 매수만 해보는 경우의 결과를 보여줍니다.

강화학습 주식투자 예 - 매수만 하는 경우

지점	종가(원)	행동	보유 주식 수	누적 손익률	보상 결정	누적 보상
1	791,000	매수	1	0%	-	매수[+1], 매도[0]
2	866,000	매수	2	0.75%	-	매수[+1], 매도[0]
3	824,000	매수	3	-0.09%	-	매수[+1], 매도[0]
4	960,000	매수	4	3.99%	보상 +1	매수[-1], 매도[0]
5	880,000	매수	5	0.79%	보상 -1	매수[-1], 매도[0]
6	813,000	매수	6	-2.56%	보상 -1	매수[-1], 매도[0]
7	810,000	매수	7	-2.74%	-	매수[-1], 매도[0]
8	767,000	매수	8	-5.75%	보상 -1	매수[-1], 매도[0]
9	783,000	매수	9	-4.47%	-	매수[0], 매도[0]
10	765,000	매수	10	-6.09%	-	매수[0], 매도[0]

이렇게 매수만 해 보니 4번 시점에서 2%가 넘는 3.99%의 수익이 발생하여 1~3번에서 했던 행동들을 +1로 보상하고, 5번 시점에서 -3.2% 손실이 발생하여 직전인 4번 행동을 -1로 보상합니다. 이런 식으로 10번까지 매수를 하면서 수익률 변동에 따라 보상을 주고 나면 각 괄호에 표시한 대로 누적 보상이 생깁니다.

다음 표에서는 이전에 받은 보상을 기반으로 매수와 매도를 결정합니다. 매수와 매도의 누적 보상이 같을 경우에 매수를 선택했습니다.

강화학습 주식투자 예 - 두 번째 학습 과정

지점	종가(원)	행동	보유 주식 수	누적 손익률	보상 결정	누적 보상
1	791,000	매수	1	0%	-	매수[+2], 매도[0]
2	866,000	매수	2	0.75%	-	매수[+2], 매도[0]
3	824,000	매수	3	-0.09%	-	매수[+2], 매도[0]
4	960,000	매도	2	3.99%	보상 +1	매수[-1], 매도[-1]
5	880,000	매도	1	2.39%	-	매수[-1], 매도[-1]
6	813,000	매도	0	1.72%	보상 -1	매수[-1], 매도[0]
7	810,000	매도	0	1.72%	-	매수[-1], 매도[0]
8	767,000	매도	0	1.72%	-	매수[-1], 매도[0]
9	783,000	매수	1	1.72%	-	매수[0], 매도[0]
10	765,000	매수	2	1.54%	-	매수[0], 매도[0]

처음 매수만 결정했을 때보다는 투자를 잘하는 것 같습니다. 여기서도 보상을 해보겠습니다. 4번 지점에서 3.99% 수익이 생겨서 직전 행동까지 +1을 보상합니다. 6번 지점에서는 4번 지점 대비 -2.2%의 손실이 생겨서 직전 행동까지 -1을 보상합니다.

그런데 잘 보면 4번 지점과 5번 지점에서는 행동 결정을 잘했는데도 -1로 보상을 받습니다. 이러한 문제는 학습을 반복적으로 진행하다 보면 대부분 해결됩니다. 이 상태에서 다시 누적 보상을 보고 투자를 진행해 보겠습니다. 그 결과는 다음 표와 같습니다.

강화학습 주식투자 예 - 세 번째 학습 과정

지점	종가(원)	행동	보유 주식 수	누적 손익률	보상 결정	누적 보상
1	791,000	매수	1	0%	-	매수[+3], 매도[0]
2	866,000	매수	2	0.75%		매수[+3], 매도[0]
3	824,000	매수	3	-0.09%		매수[+3], 매도[0]
4	960,000	매수	4	3.99%	보상 +1	매수[-2], 매도[-1]
5	880,000	매수	5	0.79%	보상 -1	매수[-2], 매도[-1]
6	813,000	매도	4	-2.56%	보상 -1	매수[-1], 매도[0]
7	810,000	매도	3	-2.68%	-	매수[-1], 매도[0]
8	767,000	매도	2	-3.97%	-	매수[-1], 매도[0]
9	783,000	매수	3	-3.65%	-	매수[0], 매도[0]
10	765,000	매수	4	-4.19%	-	매수[0], 매도[0]

4번 지점과 5번 지점에서 누적 보상이 매수는 -2, 매도는 -1로 다시 매도의 보상이 더 높아 졌습니다. 최종적으로 2번째 학습 과정에서의 행동 결정을 하게 학습됐습니다. 이제는 더 학습해도 똑같은 결과만 얻게 될 것입니다.